0.序

你可能会好奇社交网络中人与人之间的好友关系是如何存储的，地图上城市与城市之间交通网络是如何建模的，实际上他们都利用了图结构，本文让我们走进基础图论,去了解图。

1.图的基础概念

1.1 图的定义

图是对若干对象之间成对关系建模的数据结构。由节点或节点（Vertex简称v），边（Edge简称e）组成。

节点集合表示:

V={v1，v2，v3,...，v7}

边集合表示:

E={e1,2，e1,3，e1,4，...，e6,7}

例如边e1,2表示连接节点v1，v2的边

图表示:

G=(V，E)

图是节点和边组成的二元组

2.图的分类

2.1无向图

无向指图中边是没有方向的，如下图e1,2可以表示节点v1到节点v2，也可以表示节点v2到节点v1。

在无向图中用“度”表示一个节点有多少条边，例如节点v1有3条边，它的度为3。

2.2 有向图

有向指图中的边是有方向且单向的，如下图e1,2表示节点v1到节点v2，从节点v2到达不了节点v1。

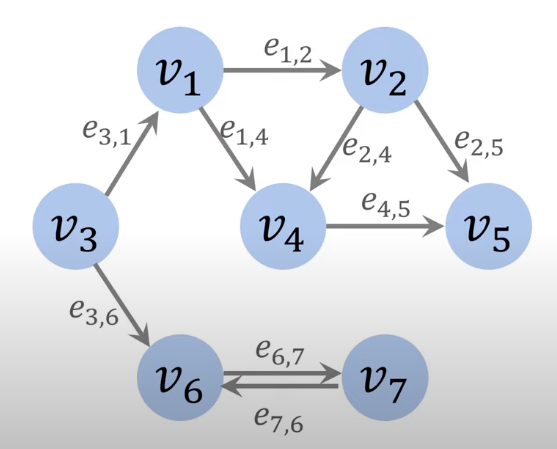
在有向图中将度分为了入度和出度

入度：节点的入度表示有多少条边指向这个节点。

出度：节点的出度表示有多少条边是以这个节点为起点指向其它节点。

2.3 无权图

无权图中，所有边的权重都是一样的。

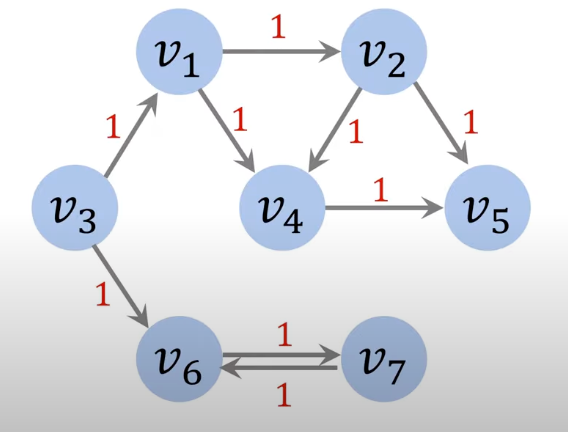
2.4 带权图

在带权图中，每条边都有一个权重，权重大小各不相同

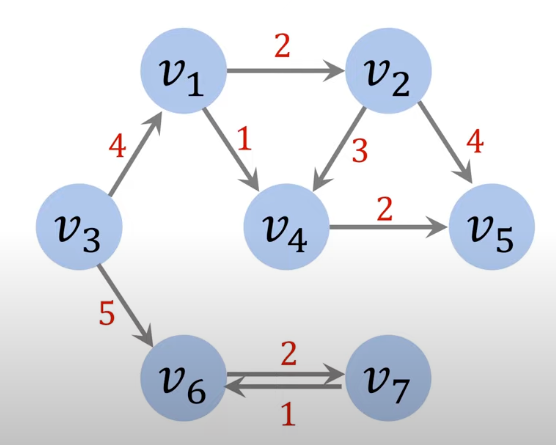
权重：

图应用不同的场景，权重的意义则不一样。

例如在城市地图中，城市和城市可以看做节点，城市和城市之间的公路可以看做边，边的权重可以是城市和城市之间的距离，距离越远权重越大。如果两地没有边则权重记作无穷大。

3.图的存储方式

图只是逻辑上的概念，将实体的关系映射到一张图上，实际存储操作本质还是数组+链表。

3.1 邻接矩阵

邻接矩阵底层依赖一个二维数组。

以无向无权图为例

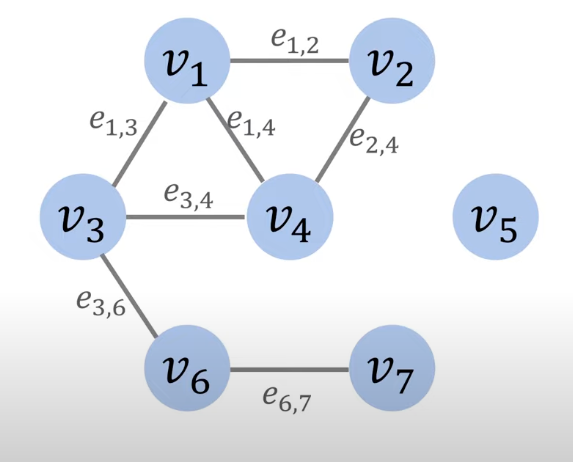
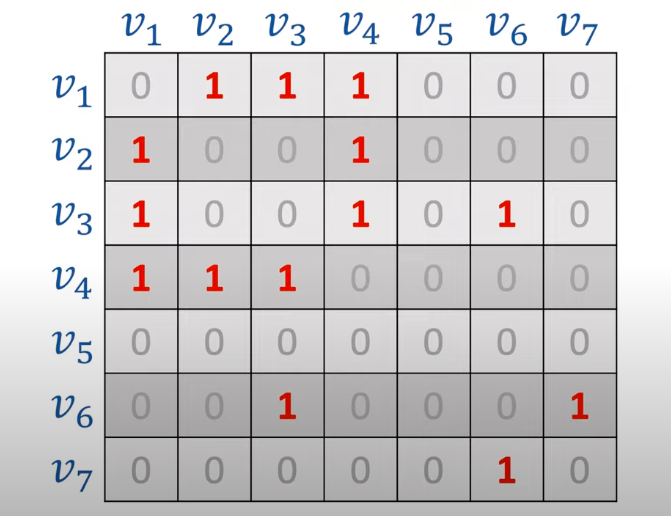
如图中有7个节点，所以邻接矩阵的大小为7*7，第i行和第j列对应节点vi，例如下图圈出第6列第6行对应图节点v6，二维数组中的值表示权重。如果两个节点有边则权重为1，无边则权重为0或正无穷。

可以发现v3节点到v6节点，由于是无向图，有相反两个方向，所以对应邻接矩阵中两个元素，表示2个权重，权重相同都为1，这里可以发现无向图都是对称的。

再或者以有向无权图为例

邻接矩阵如下

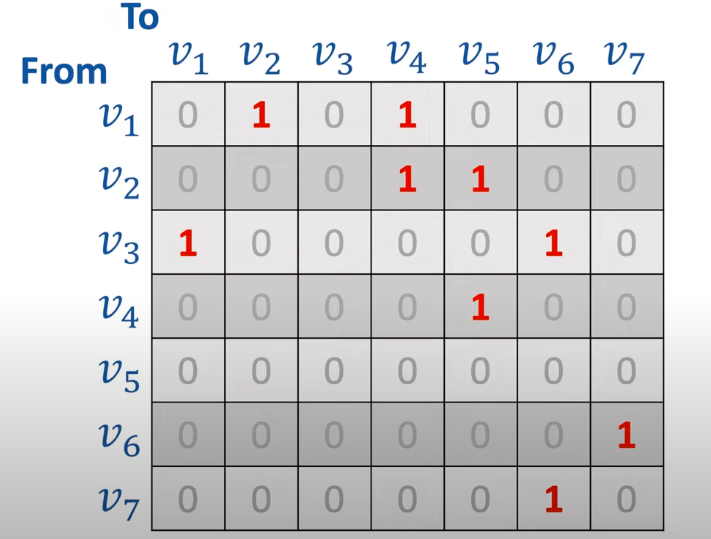
以无向有权图为例

边的权重不相同

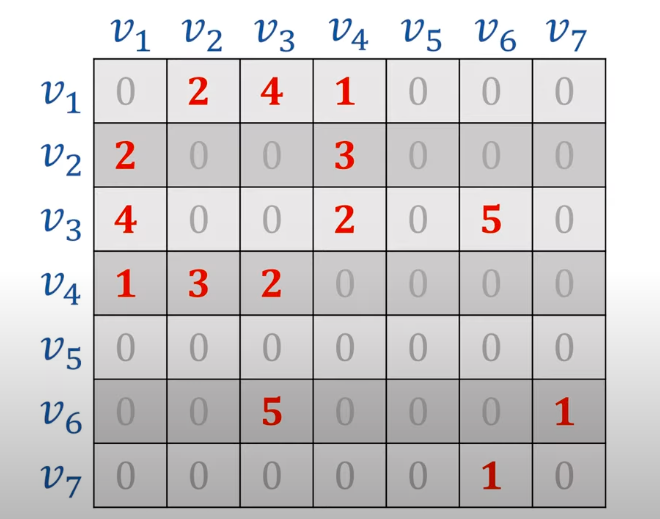
可以发现临街矩阵存储方式缺点比较浪费空间，优点是查询效率高，方便矩阵运算。

3.2 邻接表

针对邻接矩阵比较浪费内存空间的问题，来看另一种图的存储方式，邻接表。

类似散列表，每个节点对应一条链表，链表中存储和这个节点相连接的其它节点。

以无向无权图为例

如上图中

v3节点与v1，v4，v6节点相连，所以v3节点对应的链表关联v1，v4，v6节点，记为1，4，6。

v5节点和任何节点都不想连，所以记为空。

邻接表存储虽然比较节省空间，但是使用相对会比较耗时间，例如我想确定是否有一条节点v1到节点v4的边，就需要遍历节点v1的链表，找到链表中是否存在节点v4。

如果链表过长为提高效率，可以将链表换成其它高效的数据结构，例如平衡二叉树，红黑树，跳表等。

4.图存储代码事例

4.1 邻接矩阵事例代码

public class AdjacencyMatrix {

    /**
     * 矩阵
     */
    private final int[][] matrix = new int[20][20];

    /**
     * 城市节点
     */
    private final City[] cityVertexList = new City[20];

    /**
     * 当前节点下标
     */
    private int currentVertIndex;

    /**
     * 是否为有向图
     */
    private final boolean directed;

    public AdjacencyMatrix(boolean directed) {
        this.currentVertIndex = 0;
        this.directed = directed;
    }

    /**
     * 增加城市节点
     *
     * @param city
     */
    public void addVertex(City city) {
        cityVertexList[currentVertIndex++] = city;
    }

    /**
     * 城市和城市之间添加边
     *
     * @param cityNameStart
     * @param cityNameEnd
     */
    public void addEdge(String cityNameStart, String cityNameEnd) {
        int startIndex = findCityIndexByName(cityNameStart);
        int endIndex = findCityIndexByName(cityNameEnd);
        if (startIndex == endIndex) {
            return;
        }
        matrix[startIndex][endIndex] = 1;
        if(!directed){
            matrix[endIndex][startIndex] = 1;
        }
    }

    private int findCityIndexByName(String cityName) {
        for (int i = 0; i < cityVertexList.length; i++) {
            if (cityVertexList[i] == null) {
                throw new IllegalStateException("未找到该城市节点");
            }
            if (cityVertexList[i].getCityName().equals(cityName)) {
                return i;
            }
        }
        throw new IllegalStateException("未找到该城市节点");
    }

    /**
     * 打印矩阵
     */
    public void printMatrix() {
        for (int i = 0; i < currentVertIndex; i++) {
            for (int j = 0; j < currentVertIndex; j++) {
                System.out.print(matrix[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        AdjacencyMatrix matrix = new AdjacencyMatrix(true);
        matrix.addVertex(new City("成都"));//0
        matrix.addVertex(new City("北京"));//1
        matrix.addVertex(new City("吉林"));//2
        matrix.addVertex(new City("杭州"));//3
        matrix.addEdge("成都", "吉林");//02
        matrix.addEdge("吉林", "杭州");//23
        matrix.addEdge("杭州", "北京");//31
        matrix.addEdge("北京", "成都");//10
        matrix.printMatrix();
    }

}

4.2 邻接表代码

/**
 * @description： 图-邻接表
 * @Author MRyan
 * @Date 2022/10/15 22:14
 * @Version 1.0
 */
public class AdjacencyList {

    /**
     * 节点集合
     */
    private final Node[] nodes;

    /**
     * 邻接表中表对应的链表的节点
     */
    private static class ENode {
        /**
         * 该边所指向的节点的位置
         */
        ENode nextEdge;

        /**
         * 指向下一条弧的指针
         */
        int iVex;
    }

    /**
     * 邻接表中表的节点
     */
    private static class Node {
        /**
         * 节点信息
         */
        ENode firstEdge;

        /**
         * 指向第一条依附该节点的弧
         */
        String data;
    }


    /**
     * 创建图(用已提供的矩阵)
     *
     * @param vertex   节点数组
     * @param edges    边数组
     * @param directed 是否是有向图
     */
    public AdjacencyList(String[] vertex, String[][] edges, boolean directed) {
        // 初始化"节点数"和"边数"
        int vLen = vertex.length;
        // 初始化"节点"
        nodes = new Node[vLen];
        for (int i = 0; i < nodes.length; i++) {
            nodes[i] = new Node();
            nodes[i].data = vertex[i];
            nodes[i].firstEdge = null;
        }
        // 初始化"边"
        for (String[] edge : edges) {
            // 读取边的起始节点和结束节点
            int p1 = getPosition(edge[0]);
            // 读取边的起始节点和结束节点
            int p2 = getPosition(edge[1]);
            // 初始化node1
            ENode node1 = new ENode();
            node1.iVex = p2;
            // 将node1链接到"p1所在链表的末尾"
            if (nodes[p1].firstEdge == null) nodes[p1].firstEdge = node1;
            else linkLast(nodes[p1].firstEdge, node1);
            if (!directed) {
                // 初始化node2
                ENode node2 = new ENode();
                node2.iVex = p1;
                // 将node2链接到"p2所在链表的末尾"
                if (nodes[p2].firstEdge == null) nodes[p2].firstEdge = node2;
                else linkLast(nodes[p2].firstEdge, node2);
            }
        }
    }

    /*
     * 将node节点链接到list的最后
     */
    private void linkLast(ENode list, ENode node) {
        ENode p = list;
        while (p.nextEdge != null) p = p.nextEdge;
        p.nextEdge = node;
    }

    /*
     * 返回节点位置
     */
    private int getPosition(String ch) {
        for (int i = 0; i < nodes.length; i++)
            if (Objects.equals(nodes[i].data, ch)) return i;
        return -1;
    }

    /*
     * 打印矩阵队列图
     */
    public void print() {
        for (int i = 0; i < nodes.length; i++) {
            System.out.printf("%d(%s): ", i, nodes[i].data);
            ENode node = nodes[i].firstEdge;
            while (node != null) {
                System.out.printf("%d(%s) ", node.iVex, nodes[node.iVex].data);
                node = node.nextEdge;
            }
            System.out.println();
        }
    }

    public static void main(String[] args) {
        String[] vertex = {"成都", "北京", "吉林", "杭州", "乌鲁木齐", "重庆", "呼和浩特"};
        String[][] edges = new String[][]{{"成都", "吉林"}, {"吉林", "杭州"}, {"杭州", "北京"}, {"北京", "成都"},};
        // 采用已有的"图"
        AdjacencyList pG = new AdjacencyList(vertex, edges, true);
        // 打印图
        pG.print();
    }
}

5.图的应用

简单的介绍了图的基础概念，以及图结构，下面回到我们开头的问题：如何存储社交网络中的好友关系。

最基本需要支持如下几种场景：

• 某个用户的粉丝有哪些用户
• 某个用户关注了哪些用户

因为社交网络是一张稀疏图，使用邻接矩阵存储相对比较浪费存储空间，所以使用邻接表来存储。

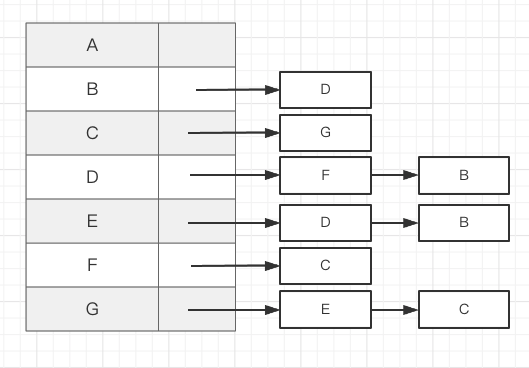
通过邻接表存储有向图可以很轻松的查找某个用户关注了哪些用户，如下图：

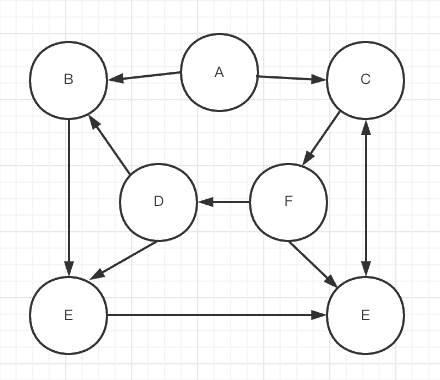
邻接表表示如下：

基于邻接表可以轻松的查找某个用户关注了哪些用户。

那如何查找某个用户被哪些用户关注呢，可以从逆邻接表中查找。

邻接表存储的是用户的关注关系，而逆邻接表存储用户的被关注关系。

对于小规模的数据，可以将整个社交关系模型存储在内存中，但数据规模太大，无法全部存储到内存中，可以通过哈希算法等数据分配技术，将邻接表存储在不同机器上，当查询节点和节点之间的关系时，可以通过同样的哈希算法，先定位到节点所在的机器，然后再对应机器上查找。

当然也可以持久化到外部存储上。

参考

http://wangshusen.github.io/

作者：MRyan

本文采用 知识共享署名-相同方式共享 4.0 国际许可协议 进行许可。
转载时请注明本文出处及文章链接。本文链接：https://www.wormholestack.com/archives/607/